Ein PID-Regler (Proportional Integral Derived) ist ein Gerät, das die Regelung eines geschlossenen Regelkreises in einem automatischen System ermöglicht. Er ist der in der Industrie am häufigsten verwendete Reglertyp, mit dem eine Vielzahl von Prozessen gesteuert werden können.
Eine kleine Anekdote zum Verständnis des Prinzips einer Regelung
Stellen Sie sich vor, Sie fahren mit Ihrem Auto auf der Autobahn und möchten Ihre Geschwindigkeit auf 130 km/h festlegen. In der Praxis wird Ihnen dies ohne große Probleme gelingen. In diesem Beispiel ist es wichtig zu verstehen, wie Ihr Geist es schafft, Ihre Geschwindigkeit intuitiv zu regulieren.
Regel 1: Proportionale Aktion
Wenn Sie auf der Autobahn mit einer bestimmten Geschwindigkeit fahren wollen, ist das Naheliegendste, Sie sich zu sagen: “Je langsamer ich im Vergleich zur gewünschten Geschwindigkeit fahre, desto stärker trete ich auf das Gaspedal“. Der Druck auf das Gaspedal ist also proportional zur Differenz zwischen der gewünschten und der tatsächlichen Geschwindigkeit.
Wenn Sie auf der Autobahn mit einer bestimmten Geschwindigkeit fahren wollen, ist das Naheliegendste, Sie sich zu sagen: “Je langsamer ich im Vergleich zur gewünschten Geschwindigkeit fahre, desto stärker trete ich auf das Gaspedal”. Der Druck auf das Gaspedal ist also proportional zur Differenz zwischen der gewünschten und der tatsächlichen Geschwindigkeit.
Mit dieser Methode treten Sie also bei einer Geschwindigkeit von 50 km/h voll auf das Gaspedal. Ihre Geschwindigkeit steigt schnell an und nähert sich der gewünschten Geschwindigkeit. Sobald Sie 130 km/h erreicht haben, geht der Fehler auf null zurück und Sie gehen vom Gas. Danach hat man aufgrund des Trägheitseffekts des Autos die Sollgeschwindigkeit überschritten.
Wenn Sie das Gaspedal loslassen, beginnt das Auto zu verlangsamen, bis es wieder unter die Sollgeschwindigkeit fällt. Sie beginnen also wieder, das Gaspedal ein wenig zu betätigen, dann nach und nach immer mehr, um die 130 km/h zu erreichen. Schließlich gelingt es Ihnen, Ihre Geschwindigkeit bei einer niedrigeren als der von Ihnen eingestellten Geschwindigkeit zu stabilisieren, sagen wir 120 km/h.
Regel 2: Integrale Aktion
In diesem Moment denken Sie: “ Verflixt! Ich kann die gewünschte Geschwindigkeit nicht erreichen. Ich muss eine weitere Regel in meine Überlegungen einbeziehen! “. Sie beschließen, dass Sie, wenn Ihre Geschwindigkeit lange unter dem Zielwert bleibt, immer stärker beschleunigen. Das heisst, dass Sie nicht nur proportional zum momentanten Abweichung beschleunigen, sondern diese Abweichung über die Zeit zu summieren. Je größer diese Summe ist ist, desto mehr beschleunigen Sie.
Wenn Sie also Ihre Geschwindigkeit bei 120 km/h stabilisieren, steigt der Gesamtfehler an und Sie beginnen, immer stärker auf das Gaspedal zu treten, bis Sie 130 km/h erreichen und überschreiten. Bei 130 km/h ist die Fehlersumme nach wie vor positiv, also treten Sie weiter auf das Gaspedal.
Bei mehr als 130 km/h ist der momentane Fehler negativ und verringert somit die Fehlersumme. Sie nehmen also den Fuß immer stärker vom Gas, bis Sie wieder 130 km/h erreichen.
Bei 130 km/h ist der Fehler wieder negativ und Sie verzögern weiter. Sie beschleunigen also wieder, bis Sie schließlich nach vielen Schwankungen bei 130 km/h bleiben.
Regel 3: Abgeleitete Aktion
Bei einer Geschwindigkeit von 130 km/h angekommen, denken Sie: “Das war’s, ich bin da! Aber ich war nicht sehr effizient … Müsste ich nicht noch eine dritte Regel hinzufügen, um noch besser zu sein? “. Deshalb beschließen Sie, Ihre Geschwindigkeit vorherzusehen. Je näher Ihre Geschwindigkeit an der optimalen Geschwindigkeit liegt, desto weniger beschleunigen Sie, und umgekehrt!
Wenn Sie sich also schnell der 130 km/h-Marke nähern, beeilen Sie sich, den Fuß vom Gas zu nehmen, um die 130 nicht zu abrupt zu überschreiten. Wenn Sie also vorausschauend fahren, verringern Sie das Phänomen des Aufschaukelns und Sie etablieren sich schneller bei der gewünschten Geschwindigkeit!
So, jetzt haben Sie intuitiv eine PID-Regelung geschaffen!
Allgemeines Prinzip
Der beobachtete Fehler ist die Differenz zwischen dem zu erreichenden Sollwert und der direkten Messung.
Der PID ermöglicht 3 Aktionen zur Kompensierung dieses Fehlers:
- Proportional: Der Fehler wird mit einer Verstärkung G multipliziert.
- Integral: Der Fehler wird über ein Zeitintervall s summiert und dann mit einer Verstärkung Ti multipliziert.
- Derived: Der Fehler wird nach einer Zeit abgeleitet und dann mit einer Verstärkung Td multipliziert.
Es gibt mehrere mögliche PID-Architekturen, um die drei Effekte zu kombinieren (seriell, parallel oder gemischt).
Die unten dargestellte parallele Konfiguration ist die am weitesten verbreitete.
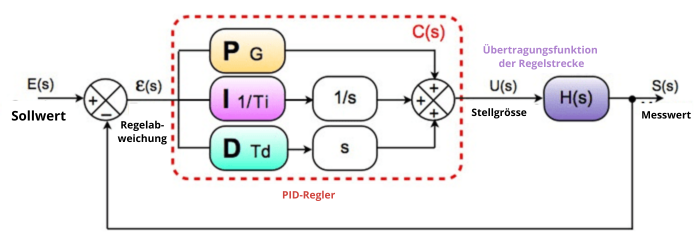
1) Die Proportionale Aktion :
Die proportionale Aktion erlaubt die Beeinflussung der Reaktionsgeschwindigkeit des gesteuerten Prozesses.
Je höher die Verstärkung, desto schneller die Reaktion, und desto geringer der statische Fehler (bei reiner Proportionalität), aber gleichzeitig verschlechtert sich die Stabilität.
Es muss also ein Kompromiss zwischen Reaktionsgeschwindigkeit und Stabilität des Prozesses gefunden werden.

2) Die integrierende Aktion :
Die integrierende Aktion ermöglicht es, den statischen Fehler (die Abweichung zwischen Messwert und Sollwert) zu beseitigen.
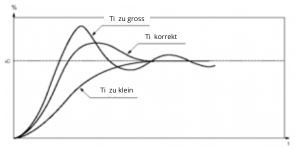
Je höher die integrierende Aktion ist (TI klein), desto schneller wird die Reaktion und desto schlechter die Stabilität.
Auch hier gilt es also, einen guten Kompromiss zwischen Geschwindigkeit und Stabilität zu finden.
3) Die abgeleitete Aktion :
Die abgeleitete Aktion ist antizipierend. Sie fügt nämlich einen Term hinzu, der die Geschwindigkeit berücksichtigt, mit der sich die Abweichung ändert. Dies ermöglicht eine vorausschauende Reaktion, wobei Reaktion des Prozesses beschleunigt wird, wenn die Abweichung zunimmt.
Je höher die abgeleitete Aktion ist (Td groß), desto schneller reagiert der Prozess.
Auch hier gilt es, einen guten Kompromiss zwischen Geschwindigkeit und Stabilität zu finden.

4) Die Aktion PID - Proportional, Integral, Derivated :
Diese Abbildung verdeutlicht die Wirkung der einzelnen Regelaktionen auf ein und dasselbe geregelte System.
- Schnelligkeit gewährleisten: Aktion P
- den statischen Fehler aufheben: Aktion I
- die Stabilität verbessern: Aktion D

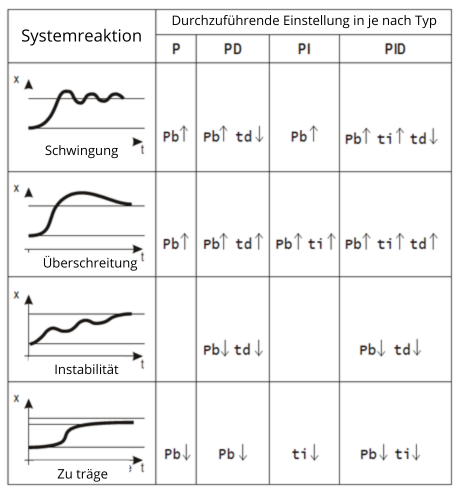
Methode zur Einstellung der PID-Parameter :
Manuelle Methode :
- Wenn der Prozess in der Produktion bleiben soll, besteht eine Methode der Einstellung darin, die Werte Integral (I) und Ableitung (D) auf null zu setzen.
- Erhöhen Sie dann die Proportionalverstärkung (P), bis der Ausgang beginnt zu oscillieren.
- Erhöhen Sie dann die Integralverstärkung, bis die Oszillation aufhört.


 Blog
Blog

